Cardiac modeling

The human heart is a sophisticated machine, finely tuned by millions of years of evolution, whose functional role is pumping the blood throughout to body cells. Mathematical and numerical modeling are increasingly recognized as valuable tools in cardiovascular research and computational medicine, with the twofold role of deepening our understanding of the cardiac function and of improving patient care by providing clinicians with patient-specific quantitative information.

Modeling active force generation at the microscale.

I am interested in the mathematical modeling of the subcellular processes whereby cardiac muscle cells convert the chemical energy of ATP into mechanical work. These physical processes have a biochemical and mechanical nature, and require stochastic calculus tools for their understanding. This makes it challenging to describe them in a mathematical formalism that is compact enough to be used in a multiscale context. Moreover, what makes this field even more fascinating is that many of the mechanisms that regulate the force generation process have not yet been understood on the biophysical level, and mathematical modeling can be a key tool to shed light on them and enhance their understanding.

In this context, I developed a microscopic model of active force generation, freely available in this repository, and illustrated in my PhD Thesis, which was awarded through several prizes (IJNMBE Best PhD Award in Biomedical Engineering, ECCOMAS Best PhD Thesis Award, Best VPHi Thesis Award in In Silico Medicine, GBMA PhD Award 2020, VPH2020 Young Investigator Award). This model allowed for the first time to include a mechanistic description of calcium-driven cooperative activation in multiscale simulations.

Multiscale heart modeling.

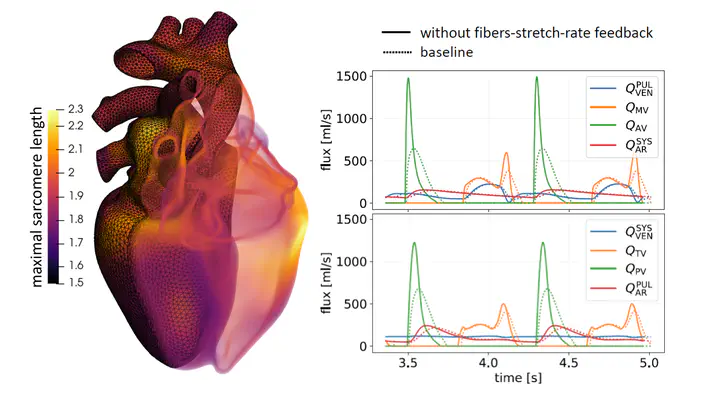
In addition to developing models at the subcellular scale, I am interested in developing multiscale models for the overall cardiac function, including electrophysiology, tissue mechanics, fluid dynamics, and myocardial perfusion. These physical processes are described by systems of Ordinary and Partial Differential Equations, coupled together in a complex network of interactions and regulatory feedbacks. The numerical simulation of these processes is extremely challenging, because of their multiscale nature, and because of the numerical difficulties that arise when coupling different core models together. I am also interested in issues related to the patient-specific calibration of such models, which requires solving inverse problems that exploit data from clinical exams and medical imaging.

Among my contributions in this area I mention the introduction of new energy-consistent boundary conditions for cardiac mechanics, the development of perfusion models, and the study of algorithms to recover the stress-free configuration of the heart. I also provided a solution to a long-standing problem in cardiac mechanics by means of a new stabilized numerical scheme that removes numerical oscillations arising from the interaction between tissue mechanics and microscale force generation. This allowed for the first time in the literature to perform multiscale simulations including stretch-rate feedback, shedding light on the role this important mechanism plays in the regulation of the cardiac output. In the context of patient-specific personalization, I also introduced a semi-physical emulator and Scientific Machine Learning methods that enabled Sensitivity Analysis and Uncertainty Quantification on complex multiscale cardiac models.