Scientific Machine Learning

Scientific Machine Learning creates concrete bridges and synergies between Machine Learning and Scientific Computing. By blending physics-based methods and data-driven models, it is indeed possible to accelerate traditional numerical schemes and improve the accuracy and generalization of Machine Learning algorithms, leveraging at the same time data and physical knowledge.

Machine Learning based surrogate models for differential problems

The numerical approximation of models based on differential equations typically calls for large computational resources and significant resolution times, which often do not meet the requirements of real-life applications. Based on this motivation, I am interested in the development of Machine Learning methods for constructing reduced order models that surrogate high-fidelity solvers of differential equations. These are particularly useful in many-query contexts, such as sensitivity analysis, uncertainty quantification e robust parameter estimation.

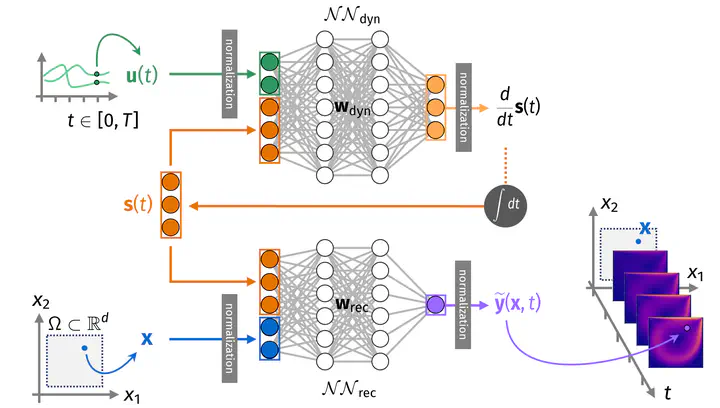
Specifically, I have developed a method capable of learning a time-dependent differential equation from input-output data, that I then applied to multiscale and multiphysics cardiac problems, thus enabling sensitivity analysis and uncertainty quantification. Furthermore, I have worked on USM-Nets, a class of neural networks capable of predicting the solution of PDEs in domains of variable shapes, and on LDNets, neural network models that learn the space-time dynamics of PDEs with excellent generalization capabilities.

Data-driven modeling

When the physical understanding of the principles governing a natural or industrial process is limited compared to the amount of available data, it makes sense to build (or, better, to learn) a model in a data-driven manner, rather than relying on first principles. Since the problem is formally analogous to training a surrogate model from synthetically generated data, the methodologies mentioned in the previous section are well-suited for this purpose. Additionally, I have worked on a framework that combines model learning with data assimilation for constructing data-driven models for multiscale temporal dynamics. This applies in cases where there is a physical understanding of the fast dynamics but not the slow dynamics, which may be related to processes such as remodeling or growth.

Neural Network based methods for the approximation of differential problems

Thanks to the universal approximation property of artificial neural networks, the latter are promising tools to approximate the solution of differential equations, both in the context of forward and inverse problems. In particular, I have addressed the use of multi-fidelity methods to enhance the accuracy of Physics Informed Neural Networks in low-data or high-noise regimes.